13776 работ.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z Без автора
ГЛАВА IV. Объем и содержавшие понятий. Отношения между понятиями
Глава IV.
Объем и содержание понятий.
Отношения между понятиями.
§ 45. Совокупность единичных предметов, обозначаемых общим понятием, называется классом. Совокупность единичных понятий (или единичных представлений), обозначающих эти предметы, называется объемом понятия: так, напр., объем понятия человек образуют единичные представления Сократа, Перикла, Шекспира, этого Фомы, Семена и т. д. и т. д. (т. е. все люди); точно также объем понятия плоский треугольник составляет единичное понятие (или представление) треугольника, образуемого в такой-то момент времени воображаемыми прямыми, соединяющими центр Земли, Солнца и Юпитера, единичное понятие (или представление) воображаемого треугольника, конструируемого при определении расстояния какого-либо недоступного предмета и т. д., и т. д. до бесконечности (все треугольники). Объем общего понятия может быть получен также из суммы объемов более частных понятий, подчиненных ему; так, напр., объем понятия плоский треугольник есть сумма объемов понятий остроугольный треугольник, прямоугольный треугольник, тупоугольный треугольник. Конечно, получить объем данного понятия из суммы объемов более частных понятий можно многими различными способами; так, напр., объем понятия треугольник слагается, как мы видели, из объемов понятий остроугольного, прямоугольного и тупоугольного треугольника, но тот же объем, очевидно, может быть получен и путем суммирования объемов понятий разностороннего треугольника, равностороннего треугольника и треугольника, имеющего две стороны, равные друг другу. Совокупность мыслимых в понятии признаков, тожественных во всех особях класса, называется содержанием общего понятия. Напр., содержание понятия плоский треугольник состоит из таких признаков, как ограниченность части плоскости тремя линиями, из того, что эти линии прямые и что они пересекаются.
Все сказанное об объеме и содержании общих понятий относится также и к общим представлениям. Единичные понятия (и представления) объема не имеют, так как означают один предмет, а не класс предметов, но содержание у них есть: мысля и представляя единичный предмет, мы, конечно, имеем в виду признаки его 1).
1) В английской литературе по логике речь идет, обыкновенно, не об объеме и содержании понятий и представлений, а о значении и соозначении имен. Отсюда объясняются некоторые особенности учений английских логиков. См., между прочим, интересные соображения Бозанкета о соозначении (содержании) собственных имен («Основания логики», 1914, стр. 93-99).
107
Количество особей, входящих в состав общего понятия, может быть ограниченным, но может быть также бесконечно большим или неопределенно большим. В первом случае понятие называется регистрирующим (можно было бы составить реестр особей, подходящих под понятие), а во втором будем называть понятие бесконечным. Так, понятия Апостол Иисуса Христа, государство XIX века, французский солдат, участвовавший в войне 1914—1918 г. принадлежат к числу регистрирующих, а понятия треугольник, человек, государство, солдат, принадлежат к числу бесконечных. Обыкновенно, наличность пространственно-временных признаков в содержании понятия придает ему характер регистрирующего понятия.
Объем общего понятия (и представления) символически изображается, обыкновенно, посредством круга или посредством части круга. Соответственно этому следовало бы условиться символически изображать значение единичного понятия (и представления) посредством точки. Этим символам можно придать следующий смысл: на площади круга А, выражающего объем данного понятия, напр., человек, собрались все особи, образующие класс человек, так что за пределами окружности этого круга нигде в мире не осталось ни одного действительного и возможного человека.
Поместить все особи на площади круга можно даже и в том случае, если множество их есть актуальная или потенциальная бесконечность, потому что мы обозначаем их точками, а точек на площади можно поместить бесконечное множество. Благодаря своей наглядности этот символ есть превосходное средство для выражения некоторых логических отношений между понятиями, а также соответствующих им онтологических отношений между классами или классами и особями: не следует ведь забывать, что каждое логическое отношение имеет также и онтологический смысл, согласно теориям сторонников метафизического идеал-реализма.
§ 46. Важнейшие отношения между понятиями обусловлены степенями родства между их содержаниями и объемами. С этой точки зрения, сопоставляя понятия попарно, можно все их разделить на два класса: согласимые и несогласимые или противоположные понятия.
Согласимыми называются два понятия, в содержании которых нет признаков, несовместимых друг с другом, т. е. таких признаков, которые, обладая разным содержанием, в то же время должны были бы приписываться предмету в одном и том же отношении. Поэтому логически возможно, что существуют предметы, входящие в объем как одного, так и другого понятия, т. е. объемы двух согласимых понятий хотя бы отчасти совпадают. Символически это отношение понятий выражается двумя кругами, площадь которых хотя бы отчасти совпадает или которые соприкасаются хотя бы в одной точке.
108
Наоборот, несогласимыми или противоположными называются два понятия, в содержании которых есть признаки, несовместимые друг с другом. Поэтому логически невозможно, чтобы существовал предмет, входящий в объем как одного, так и другого понятия. Символически это отношение выражается двумя кругами, площадь которых не имеет ни одной общей точки.
Между согласимыми понятиями возможны три степени родства и, следовательно, три вида отношений: тожество (объемов), подчинение и перекрещивание. Эти три отношения, расположенные по степеням убывания родства, изображаются кругами, совпадающими (тожество), включенными друг в друга (подчинение) и перекрещивающимися.
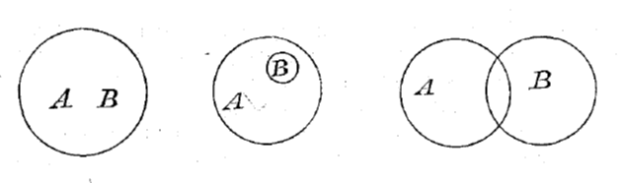
Тожественные понятия имеют одинаковый объем, но содержание у них состоит из отличных друг от друга признаков, связанных, однако, взаимно-необходимою связью, чем и объясняется тожество объемов. Таковы, напр., понятия «четверть рубля» и «двадцать пять копеек». Символ этого отношения — два совпадающие круга А и В.
Отношение подчинения существует между понятиями А и В в том случае, если содержание понятия А целиком входит в содержание понятия В, составляя часть его, а объем понятия В, наоборот, целиком входит в объем понятия А, составляя часть его. Содержание понятия А беднее содержания понятия В, но зато объем его богаче: так как оно содержит в себе меньше признаков, то большее количество особей может подходить под него. Итак, одно из этих понятий более общее, а другое более частное. Более общее называется подчиняющим, а более частное — подчиненным. Примером могут служить следующие пары понятий: позвоночное — млекопитающее; цвет — белизна; философ — Сократ.
В том случае, когда отношение подчинения существует между двумя общими понятиями, одно из них, именно более общее, называется родом, а более частное — видом. Вследствие чрезвычайной важности этого случая подчинения полезно обозначать его особым термином — родо-видовое отношение. Символическим выражением его служат два круга, из которых один включен в другой.
109
Отношение подчинения невозможно между двумя единичными понятиями, так как они оба не имеют объема. Но между общим понятием и единичным отношение подчинения возможно с тем лишь несущественным отличием от родо-видового подчинения, что здесь включен в класс не другой меньший класс, а индивидуум, и выразить это отношение символически приходится не двумя кругами, а точкой, помещенною на площади круга. Таково, напр., отношение между понятиями человек и Сократ 1).
Два или более понятия одинаковой степени общности, несогласимые друг с другом, но подчиненные одному и тому-же более общему понятию, называются соподчиненными; напр., великоросс, малоросс, белорусе — понятия, соподчиненные в отношении к понятию русский.
Перекрещивающимися называются понятия, в содержании которых есть отличные друг от друга, но совместимые признаки (т. е. признаки, которые могут принадлежать предмету в разных отношениях), не связанные друг с другом законосообразно. Объемы таких двух понятий отчасти совпадают; иными словами, возможны предметы, подходящие одновременно как под одно, так и под другое понятие. Таковы, напр., понятия: беспозвоночное — паразит; химик — композитор (так, А. П. Бородин был композитором и профессором химии); трудный — приятный (так, напр., великое научное открытие — дело трудное, но приятное) и т. п. Символически выражается отношение перекрещивания двумя перекрещивающимися кругами (схему см. выше на стр. 109).
1) Некоторые представители математической логики (напр., Пеано) устанавливают существенное различие между включением класса в класс и подчинением индивидуума классу. Они правы с точки зрения даваемого ими определения этих терминов. Но к учению, изложенному выше, соображения Пеано не относятся. В самом деле, под словом класс, как общее понятие, мы разумеем множество особей, мыслимое разделительно; отношение такого разделительного множества к более общему классу то же, что и отношение индивидуума к классу.
Для установления своего различения представители математической логики берут, правда, не пары понятий, отвлеченно взятых, а пару понятий в суждении, именно субъект и предикат суждения; напр., они утверждают, что в суждениях «все люди — разумные существа» и «Сократ — человек» отношение между классом «человек» и классом «разумные существа» не однородно с отношением между индивидуумом «Сократ» и классом «человек». И здесь, однако, если принять изложенное мною учение об общем понятии и, сверх того, еще учение о том, что связь субъекта и предиката есть связь основания и следствия, отношение в обоих суждениях окажется однородным: и в том, и в другом суждении это не отношение подчинения, а отношение необходимого следования (между понятиями «люди» и «разумность» в первом суждении и понятиями «Сократ» и человечность во втором суждении), причем под словом «все люди», если рассматриваемое суждение мыслится, как общее, подразумевается разделительно «эта», «та» особь и т. д., из которых каждая необходимо разумна.
110
Отношение между такою парою понятий может быть выражено также четырьмя частными суждениями. Напр., некоторые беспозвоночные суть паразиты, некоторые паразиты суть беспозвоночные, некоторые беспозвоночные не суть паразиты, некоторые паразиты не суть беспозвоночные.
§47. Противоположность понятий бывает двух родов — противоречащая и противная.
Противоречащими называются понятия в том случае, когда в содержании одного из них отрицается часть признаков другого и при этом отрицаемые признаки не заменяются ничем положительным (таковы понятия: целое число, не целое число; во втором из этих понятий отрицается целость, но не указывается, мыслится ли при этом дробное или смешанное число).
Противными называются понятия в том случае, когда в содержании одного из них не только отрицается часть признаков другого, но и замещается несовместимыми с ними признаками (таковы понятия: целое число, дробное число).
Понятие, противоречащее данному понятию, обыкновенно, обозначается тем же термином, что и данное понятие, с присоединением лишь к нему отрицания (напр., целое число, не целое число). Однако, и здесь, как и всегда, язык вовсе не служит однообразным и точным выражением форм мысли. Очень часто положительный термин в соединении с отрицанием «не» употребляется в речи для обозначения понятия, стоящего в отношении противной, а не противоречащей только противоположности к первоначальному понятию (так, напр., словом некрасивый обозначается не просто отрицание красоты, но и некоторая степень безобразия). Так как для логического анализа необходимо точно отличать две стадии противоположности — чистое отрицание без всякого замещения отрицаемых признаков чем бы то ни было и отрицание, сопутствуемое замещением отрицаемого признака другими признаками, то мы условимся в тех случаях, когда язык пользуется одним и тем же отрицательным термином и для противоречащих, и для противных понятий, отличать эти термины друг от друга следующим образом: писать отрицание «не» слитно с положительным термином в случае противной противоположности (красивый, некрасивый) и раздельно в случае противоречащей противоположности (красивый, не красивый).
Отношение друг к другу объемов противоположных понятий символически изображается кругами, площади которых ни в одной точке не совпадают.
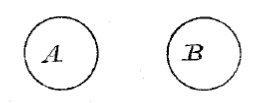
111
Так как все человеческие понятия принадлежат к единой системе человеческого мышления, то все понятия, даже противоположные друг другу, находятся в большем или меньшем родстве друг с другом. В самом деле, в содержании противоположных понятий только часть признаков исключают друг друга, среди же остальных признаков одни не противоречат друг другу, а другие даже тожественны друг другу (напр., признаки числа входят и в понятие целого числа и в понятие дробного числа). Так как в содержании всякой пары понятий есть большее или меньшее количество тожественных элементов (хотя бы, напр., тот признак, что всякая вещь, мыслимая в понятиях, есть объект мышления), то теоретически необходимо признать, что ко всякой данной паре понятий можно подыскать более общее понятие, к которому оба понятия относятся, как виды к роду, так что отношение их объемов символически должно быть выражено двумя кругами, не совпадающими друг с другом, но заключенными в третьем охватывающем их круге:
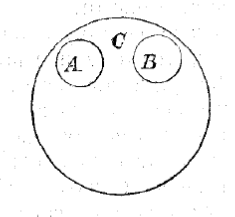
Практически такое подведение противоположных понятий под общий род, конечно, не всегда можно произвести, потому что содержания многих, в особенности наиболее общих понятий (напр., категорий), еще не подвергнуты достаточно глубокому анализу.
Чем более близки друг к другу противоположные понятия, т. е. чем больше в их содержании тожественных элементов, тем ближе стоит к ним по степени общности охватывающее их родовое понятие, напр., понятия змея и ящерица охватываются уже ближайшим более общим понятием пресмыкающееся.
Наоборот, если даны понятия, далекие друг от друга, т.е. имеющие слишком мало тожественных элементов в содержании, то родовым для них обоих может быть только понятие, очень общее сравнительно с ними. Нужен, так сказать, очень большой круг, чтобы охватить два маленьких круга, стоящих далеко друг от друга. Таковы, напр., понятия змея и сложноцветное, для которых общим родовым понятием могут служить только такие сравнительно с ними гораздо более общие понятия, как напр., организованное существо.
Противоположные понятия одинаковой степени общности, подчиненные одному и тому же родовому понятию, не слишком далеко от-
112
стоящему от них по степени общности, принято называть соподчиненными. Остальные противоположные понятия можно называть диспаратными.
Итак, мы разделили понятия на следующие группы на основании отношений родства между их содержаниями и объемами:

§ 48. Понятия можно подвергать обобщению или, наоборот, ограничению.
Обобщение понятия производится путем устранения из содержания понятия какого-либо признака (вместе с признаками, необходимо связанными с ним). Вследствие этой операции, получается понятие, относящееся к данному понятию, как род к виду; напр., если из содержания понятия квадрат устранить признак равенства углов друг другу, то понятие квадрата превратится в более общее понятие равностороннего параллелограмма; если из содержания понятия квадрат устранить признак равенства сторон, то понятие квадрата превратится в понятие прямоугольника, и т. п.
Ограничение понятия производится путем присоединения к его содержанию новых признаков, не вытекающих с необходимостью из признаков, уже заключающихся в нем. Вследствие этой операции получается понятие, относящееся к данному понятию, как вид к роду. Из понятия квадрат можно получить путем ограничения, напр., следующие понятия: квадрат, вписанный в окружность; квадрат, имеющий сторону, равную метру; сторона куба; верхнее основание усеченной правильной четырехугольной пирамиды и т. п.
Производя операции обобщения и ограничения, нетрудно усмотреть, что объем и содержание понятия находятся в обратном отношении, т. е. обогащение содержания сопутствуется уменьшением объема и наоборот. Однако, само собою разумеется, если какой-либо признак bнеобходимо связан с признаком а, так что везде, где есть а, есть и b, то в таком случае присоединение признака b к содержанию понятия, или, наоборот, не упоминание о нем не изменяет объема понятия.
113
Так, прибавка к понятию равноугольный треугольник признака разносторонности не изменяет объема понятия, следовательно, не приводит к ограничению его.
Производя ряд последовательных обобщений данного понятия и восходя таким образом к все более общим понятиям, мы получаем лестницу понятий, в которой каждая новая ступень относится к предыдущей, как род к виду. Такой ряд не может быть бесконечным; рано или поздно мы дойдем до понятия, столь бедного по содержанию или обладающего содержанием, настолько нерасчлененным в нашем сознании, что оно не может быть разложено нами дальше и потому понятие не может быть обобщено. Таковы, напр., понятия вещи, существа, качества, состояния, действия, отношения и т. п. Они называются, обыкновенно, категориями. Вопрос о том, какие именно понятия нужно считать категориями и сколько их, еще не решен. Возможно, что некоторые чрезвычайно общие понятия, заслуживающие названия категории, еще не выработаны человеческим мышлением. Поэтому не следует во что бы то ни стало стараться подвести всякое данное понятие под одну из перечисляемых в традиционной логике категорий.
Производя ряд последовательных ограничений данного понятия и нисходя таким образом к все более частным понятиям, мы получаем лестницу понятий, в которой каждая новая ступень относится к предыдущей, как вид к роду. Такой ряд понятий может быть бесконечным, если ограничению подвергается бесконечное понятие и если присоединять к его содержанию новые признаки так, чтобы получающиеся видовые понятия также были бесконечными. Напр., от понятия человек можно перейти к ряду частных понятий — образованный человек; образованный, обладающий замечательной памятью человек; образованный, обладающий замечательною памятью и сильною волею человек и т. п. без конца.
Наоборот, если для ограничения взято регистрирующее понятие или если в процессе ограничения из бесконечного получено регистрирующее понятие, то ряд актов ограничения не может быть бесконечным: рано или поздно в результате получится единичное понятие, которое, не имея объема, не может содержать под собою видов и потому не может быть далее ограничено. Напр., понятие русский может быть ограничено до предела следующим образом: русский писатель, русский писатель, родившийся в 1828 г., русский писатель, родившейся в 1828 г. и написавший роман «Война и Мир».
Предел обобщения, как мы видели, возникает вследствие невозможности дальнейшего анализа содержания понятия, а предел ограничения может явиться вследствие невозможности дальнейшего раздробления объема понятия (когда понятие не имеет объема, т. е. когда объем понятия представляет собою, так сказать, математическую точку).
114
© Гребневский храм Одинцовского благочиния Московской епархии Русской Православной Церкви. Копирование материалов сайта возможно только с нашего разрешения.
